Chapitre 17
Comment notre cerveau peut nous tromper
Par Mizel Djukic
Adapté par Walid Laaraba
Un grand pouvoir implique de grandes responsabilités.
Jusqu'à présent vous avez utilisé différents outils afin de transformer vos graphiques en histoires captivantes. Si les histoires que vous racontez parlent à votre public, elles peuvent aider à faire changer les choses et pousser les gens à agir. Mais avant d’essayer de changer le monde avec les compétences que vous avez acquises, il est important de comprendre que certaines visualisations peuvent être trompeuses en raison de la manière dont notre cerveau fonctionne.
Comment percevons-nous les différences?
Notre cerveau aime les différences. Même lorsque nous sommes en train de nous détendre devant un ordinateur en regardant des vidéos de chats et en sirotant un verre de thé glacé, notre cerveau continue de chercher des limites dans notre environnement, en identifiant les différences entre nos pieds et le sol, nos mains et le clavier, notre verre et la table. La façon dont nous percevons ces limites dépend d'une variété de facteurs dont la couleur, le contraste, la forme, et la perspective dimensionnelle de notre environnement.
Différences de couleur et de contraste
Si on parle de couleur et de contraste, le premier exemple qui nous vient à l'esprit est probablement le noir et blanc. Il est très facile pour nous de faire la distinction entre les deux car l’un est sombre et l'autre clair. La variation entre la luminosité et l'obscurité d'une couleur (connue sous le nom de « la valeur ») est une bonne façon d'établir un contraste, mais ce n’est pas la seule. Vous pouvez aussi varier la saturation de sorte que la couleur soit pâle et décolorée, ou vive et éclatante. Vous pouvez également créer un contraste en utilisant des couleurs différentes (ou teintes) qui sont faciles à distinguer les unes des autres.

La façon dont notre cerveau perçoit les contrastes dépend du contexte. Plus le contraste entre des objets est important, plus nous pensons qu’ils sont différents.Cairo, Alberto. The Functional Art. Berkeley: New Riders, 2013. Imprimé. Jetons par exemple un œil au graphique suivant:
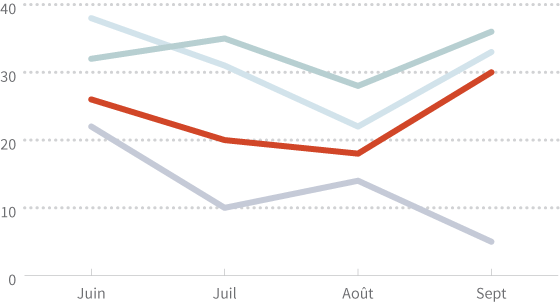
Avez-vous distingué quelque chose? Probablement la ligne rouge, et ce, pour plusieurs raisons. Observations de superhéros dans le quartierTout d'abord, la ligne rouge est plus saturée que les autres lignes. Deuxièmement, le rouge et le bleu sont des couleurs idéales pour mettre en évidence un contraste. Troisièmement, à nos yeux, le rouge et le jaune viennent au premier plan tandis que le bleu se retire vers l'arrière-plan.Rockwell, Ken. The Secret: What Makes a Great Photo. Web. 1 Mars 2014. http://www.kenrockwell.com/tech/basics.htm
En raison de la forte opposition entre la ligne rouge et le reste, notre cerveau va naturellement se concentrer sur elle, et nous allons probablement penser qu'il y a quelque chose de spécial la concernant. Avoir une ligne rouge se démarquant de cette façon est visuellement intéressant à condition qu’il y ait une bonne raison de le faire. Par exemple, si chaque ligne représentait le niveau de bonheur au fil du temps dans les différents quartiers d’une ville, la ligne rouge serait une bonne option pour mettre en évidence le bonheur d’un quartier en particulier. Par contre, si la ligne rouge ne véhicule pas de message particulier, le contraste peut mener à une importante source de confusion.
Maintenant, jetons un œil à la carte ci-dessous qui montre le niveau d'excellence dans différentes parties d'un pays appelé Relethonie:
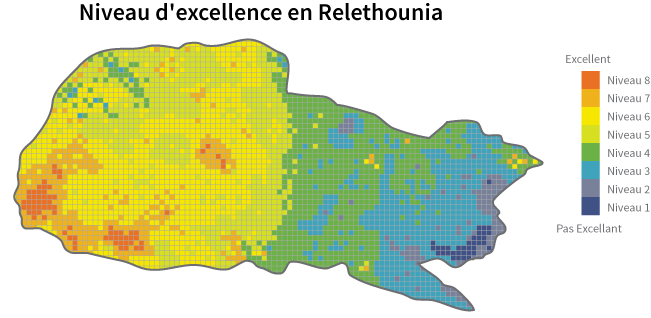
Comment interpréter ce graphique? Il semble y avoir une sorte de division entre l'est et l'ouest du pays, n’est-ce pas? En fait, cette division apparente est le résultat de l’important contraste entre les zones vertes claires et les zones vertes foncées. Il semblerait donc, qu’il y ait une plus grande différence entre ces deux parties qu’entre, par exemple, les zones jaunes et les zones vertes claires (à gauche du graphique). Mais quand on regarde la légende, on s’aperçoit que la différence entre les parties jaune et verte claire est la même que celle qui sépare les parties verte claire et verte foncée: un seul niveau d'excellence.

Une bonne pratique est de faire attention à la couleur et au contraste dans vos représentations. Quand des gens voient des zones à fort contraste dans vos graphiques, ils vont probablement y attacher une certaine importance ou penser que vous aviez l'intention de souligner un élément en le mettant en évidence avec une différence de couleurs.
DIFFÉRENCES DE FORMES
Notre cerveau a plus de mal à faire la différence entre les formes d’un graphique. Pour illustrer ce point, notez combien de temps il vous faut pour trouver le cercle rouge dans chacune des figures ci-dessous:

Adapté de: Healey, Christopher G., Kellogg S. Booth, et James T. Ennis. “High-Speed Visual Estimation Using Preattentive Processing.” ACM Transactions on Computer-Human Interaction 3.2 (1996): 4.
Avez-vous trouvé plus rapidement le cercle dans la première figure? C’est le cas pour la plupart des gens, et ce, parce que notre cerveau différencie plus facilement les couleurs que les formes. Cela est vrai même si un autre facteur est en train de changer de façon aléatoire et interfère avec ce que nous voyons.Healey, Christopher G., Kellogg S. Booth, and James T. Enns. "High-Speed Visual Estimation Using Preattentive Processing." ACM Transactions on Computer-Human Interaction 3.2 (1996): 107-135. Web. 16 Juine 2014. Par exemple, voyez combien de temps il vous faut pour trouver la limite dans chacune des figures ci-dessous:

Adapté de: Healey, Christopher G., Kellogg S. Booth, et James T. Ennis. “High-Speed Visual Estimation Using Preattentive Processing.” ACM Transactions on Computer-Human Interaction 3.2 (1996): 5.
La plupart d'entre nous trouvent la limite de couleurs (entre le rouge et le bleu) représentée dans la figure de gauche plus rapidement que la limite des formes (entre les cercles et les carrés) représentée dans la figure de droite. Dans l'image de gauche, les objets sont organisés par couleur tandis que la forme est en train de changer de façon aléatoire. L'inverse est vrai dans l'image de droite: les objets sont organisés par forme tandis que la couleur change au hasard.
Tout cela nous amène à nous questionner sur la pertinence d'utiliser des icônes et des pictogrammes dans nos visualisations étant donné que les icônes les plus simples sont définis par leurs formes, et non pas par leurs couleurs. Heureusement pour nous, le chapitre sur L'importance de la couleur, de la police et du choix des icônes répond à cette question:
La règle devrait être: Si vous pouvez clarifier quelque chose en utilisant le petit espace mis à votre disposition sans utiliser d’icône, n’en utilisez pas. [...] Dès que vous entendez quelqu’un demander “Qu’est-ce que cette icône signifie?”, vous avez perdu la bataille pour la simplicité.
Les icônes peuvent être une façon intelligente et utile d'illustrer une idée tout en assurant attrait et beauté visuelle à vos infographies, mais pour être efficaces, elles doivent trouver le juste équilibre entre le détail et la clarté. Trop de détails conduit à des icônes qui sont difficiles à distinguer les unes des autres; trop peu de détails conduit à des icônes qui sont trop abstraites. Si les formes sont trop compliquées et trop simples, cela conduit tout simplement à un public confus.
Passons à un petit exercice. Des bonnes icônes peuvent communiquer un message sans nécessairement la présence de couleurs. Chacune des trois cartes ci-dessous montre l'emplacement des hôpitaux et des bibliothèques dans une zone géographique. En se basant uniquement sur les icônes, laquelle de ces carte est la plus facile à comprendre?
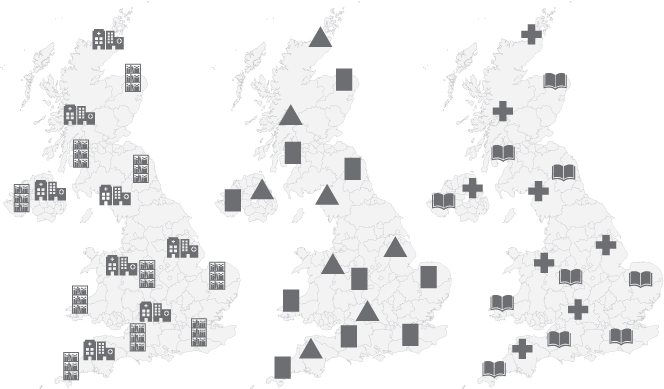
Différences de perspectives
Nous vivons dans un monde en 3 dimensions. Les objets qui nous entourent, les films que nous regardons, les jeux auxquels nous jouons, sont tous en 3 dimensions. Quand il est question de modélisation visuelle ou de cartographie, il peut être très tentant de ne pas seulement se contenter de banals graphiques à 2 dimensions. Le problème est que le résultat n’est pas toujours à la hauteur des attentes et que les lecteurs finissent plus étourdis qu’éblouis.
Comme mentionné précédemment, notre cerveau a déjà un peu de mal à distinguer les formes bidimensionnelles entre elles. Ajouter une troisième dimension à ces formes amène souvent encore plus de confusion. Afin d’illustrer ce principe, regardons deux graphiques représentant la même information. Selon vous, lequel est le plus facile à lire?
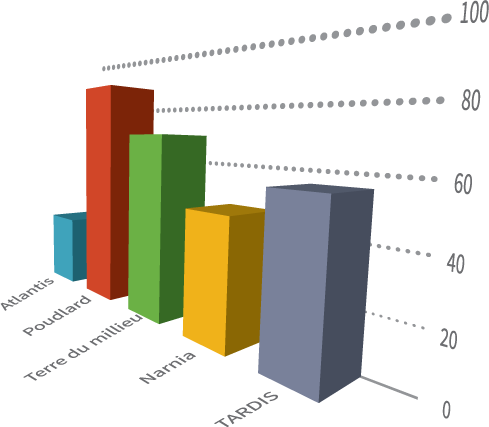
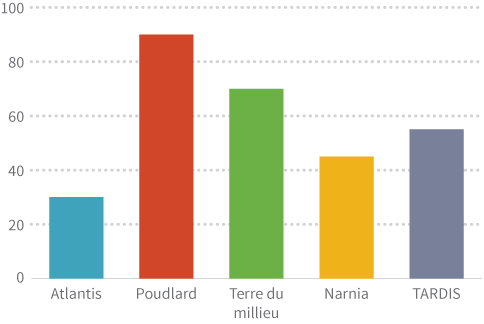
La difficulté à lire les graphiques n’est pas la seule raison d’éviter l’utilisation de visualisations en 3D. Une autre raison est d’ordre cognitif. Notre cerveau associe les différences de perspectives avec des différences de taille. Vous avez probablement déjà expérimenté ce phénomène à plusieurs reprises, que vous regardiez en bas d’une rue ou en haut d’un gratte-ciel, les objets au premier plan paraissent plus grands que ceux en arrière-plan.
Prenez par exemple une table de cuisine carrée. Vous savez que puisqu’elle est carrée, tous ses côtés ont une dimension identique. Mais en la regardant de côté, notre perception change:

Dans cette deuxième perspective, il semble que le côté le plus proche de nous est plus grand que le côté qui se trouve derrière.
Pour cette raison, de nombreux types de visualisations 3D peuvent être trompeurs. Selon vous, dans le camembert ci-dessous, quelle tranche est la plus grande: la tranche rouge ou la tranche verte? La tranche bleue ou de la tranche jaune?
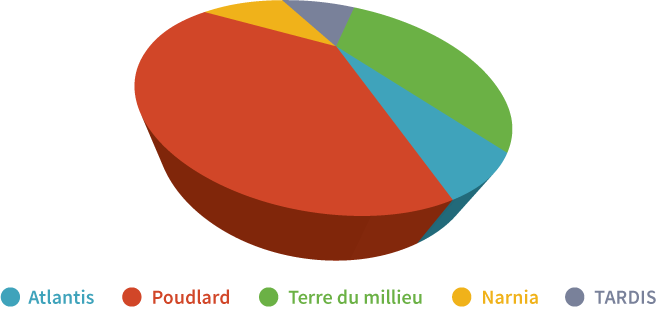
En fait, la tranche rouge et la tranche verte sont de même taille. La tranche jaune, quant à elle, est deux plus fois plus grande que la bleue. Ceci est beaucoup plus clair une fois le graphique représenté en 2 dimensions :
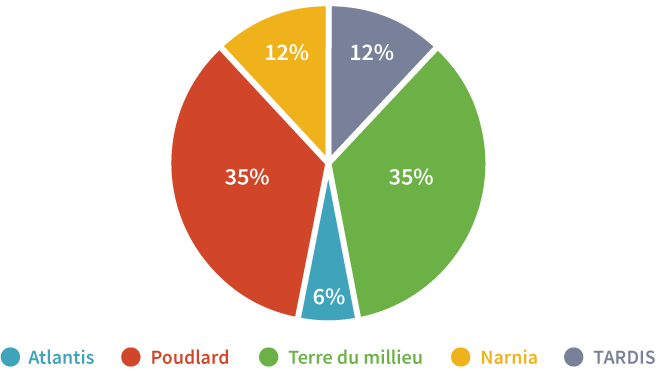
Donc, à moins d’avoir une très bonne raison d'utiliser des graphiques en 3D, il est préférable de les éviter. Mais si les graphiques en 3D ne sont pas idéaux, il existe des exceptions pour lesquelles ils peuvent être utiles. C’est par exemple le cas dans certains types de modélisations scientifiques, tels que des modèles représentant le cerveau humain ou encore de cartes qui modélisent la topographie d'une région géographique quelconque. Il existe des cas où la 3D améliore la visualisation. Assurez-vous seulement qu’elle aide à la compréhension.
Comment comparer les différences?
Qu'avons-nous appris jusqu'à présent? Que notre cerveau est très doué pour remarquer les différences de couleurs et de contrastes, mais moins pour interpréter les différences de formes et de perspectives. D'une manière générale, plus le nombre de différences dans un graphique est élevé, plus il nous faut du temps pour le comprendre. Aidons donc notre cerveau en minimisant le nombre de différences à interpréter! Pour cela, il est important d'être cohérant dans les graphiques que nous mettons en place.
Alignement constant
Notre cerveau est plutôt doué pour comparer des différences de longueur, à condition que les éléments que nous comparons partagent un point de référence commun.Cleveland, William S. and Robert McGill. "Graphical Perception and Graphical Methods for Analyzing Scientific Data." Science 229.4716 (1985): 828-833. Web. 16 Juine 2014. Essayez par exemple de comparer les longueurs des barres dans le suivant graphique :
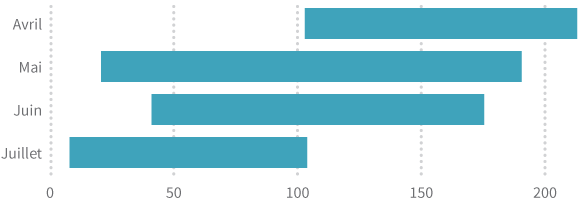
Essayez maintenant de refaire le même exercice avec le graphique ci-dessous :
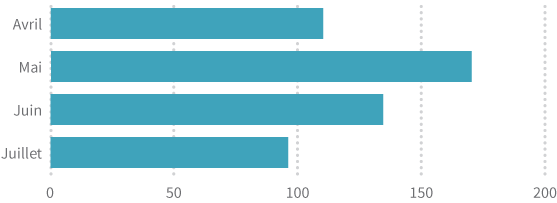
L’interprétation était plus simple avec le deuxième graphique, n’est-ce pas? Même si les deux graphiques à barres ont un axe horizontal avec les mêmes étiquettes et les mêmes marques de graduation, le deuxième graphique minimise les différences que notre cerveau doit traiter en faisant débuter toutes les barres au même niveau. Un alignement constant permet à notre cerveau de se concentrer sur les longueurs sans avoir à se soucier du point de départ de chaque barre. L’interprétation est donc plus facile.
Unités cohérentes
Il peut arriver un moment où vous voudrez représenter deux ensembles de données sur un même graphique. Exemple : un graphique à double lignes ou un diagramme à double bandes. Une idée très intéressante... tant que vous respectez le principe de cohérence.
Le graphique à barres suivant compare combien il en coûterait d’acheter des objets magiques aux États-Unis et au Royaume-Uni:
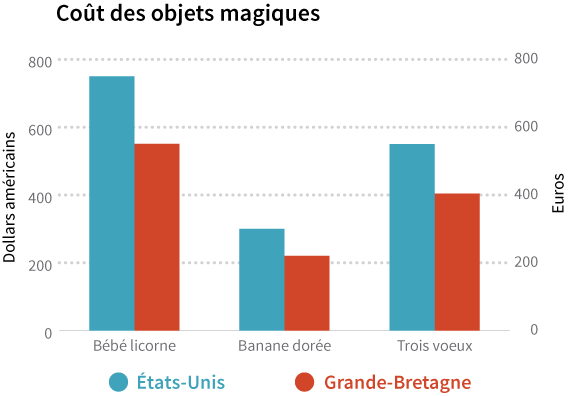
Il semble que les accessoires de magie coûtent bien moins chers au Royaume-Uni! Cependant, il faut faire attention. Se contenter de comparer les longueurs des barres rouges par rapport aux bleues n’est pas suffisant. Il y a une autre différence dont nous devons tenir compte: les unités sur les axes verticaux sont différentes. A gauche, les unités sont en dollars américains, tandis qu’à droite, les unités sont en euros. Ainsi, afin de comparer avec précision les prix entre les deux pays, nous devons soit convertir les dollars en euros, soit les euros en dollars. Certaines personnes peuvent faire ce genre de conversion de devises aisément, et ils méritent d'être félicités pour leur admirable compétence en mathématiques. Les autres vont se pencher sur cette tâche en se demandant pourquoi le designer de ce diagramme à barres est si cruel. Une bonne pratique est donc de convertir les différentes unités à des unités cohérentes afin que votre public ne soit pas obligé à le faire par lui-même :
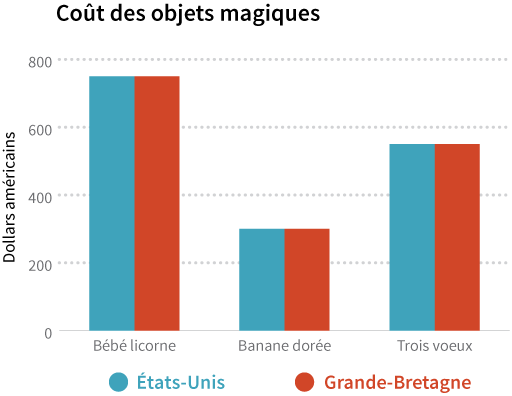
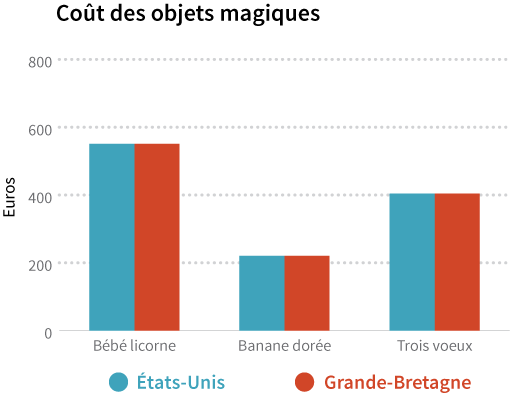
Au final, on peut constater que les objets magiques coûtent le même prix aux États-Unis et au Royaume-Uni.
Echelles cohérentes
En plus d’unités cohérentes, vos graphiques devraient aussi avoir des échelles cohérantes. Par exemple, le graphique ci-dessous compare le temps qu'il faudrait à un Terrien et à un Martien pour maîtriser leurs différents superpouvoirs:
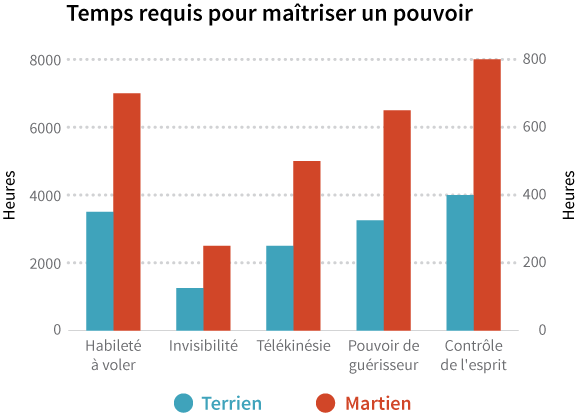
En comparant les barres, nous serions tentés de conclure que les Martiens prennent plus de temps à maîtriser leurs superpouvoirs que les Terriens, mais une fois encore, les axes verticaux sont différents. Si cette fois les unités sont conformes (les deux axes utilisent les heures comme unité), les échelles, elles, sont différentes. Sur le côté gauche, la balance est en milliers d'heures pour les Terriens, alors que sur le côté droit, la balance est en centaines d'heures pour les Martiens. Les mêmes données avec des échelles cohérentes ressembleraient à cela :
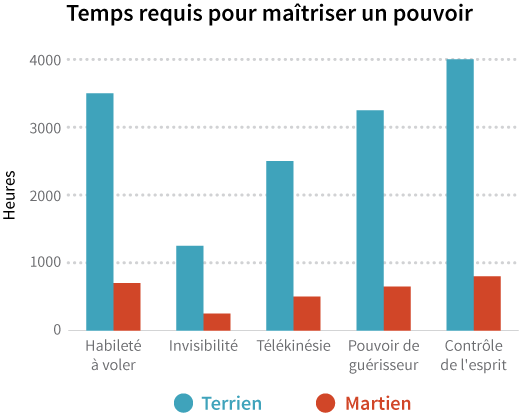
Un graphe avec des échelles cohérentes permet de constater avec évidence que les Martiens maîtrisent leurs pouvoirs beaucoup plus rapidement que les Terriens. Peut-être parce qu'ils ont moins de gravité sur leur planète, allez savoir.
Transparence
Lorsque l’on parle de visualisation de données et de transparence, il est important de garder à l’esprit que les données que l’on ne montre pas sont aussi importantes que celles qui sont affichées. Notre but principal est de donner aux lecteurs le contexte complet de la situation incluant toute information supplémentaire dont ils pourraient avoir besoin pour interpréter correctement nos graphiques.
Graphiques cumulatifs
Une valeur cumulative vous donne une information sur le combien jusqu’à maintenant. Par exemple, disons que vous voudriez garder une trace sur le nombre d’apparitions de super-héros qu’il y a dans votre quartier:
|
Mois |
Nombre d'observations de superhéros |
Nombre cumulatif d'observations de superhéros |
|---|---|---|
| Janvier | 60 | 60 |
| Févruary | 40 | 100 = 60 + 40 |
| Mars | 38 | 138 = 60 + 40 + 38 |
| Avril | 30 | 168 = 60 + 40 + 38 + 30 |
| Mai | 25 | 193 = 60 + 40 + 38 + 30 + 25 |
| Juine | 26 | 219 = 60 + 40 + 38 + 30 + 25 + 26 |
| Juillet | 20 | 239 = 60 + 40 + 38 + 30 + 25 + 26 + 20 |
| Aoûtust | 18 | 257 = 60 + 40 + 38 + 30 + 25 + 26 + 20 + 18 |
| Septembre | 30 | 287 = 60 + 40 + 38 + 30 + 25 + 26 + 20 + 18 + 30 |
| Octobre | 62 | 349 = 60 + 40 + 38 + 30 + 25 + 26 + 20 + 18 + 30 + 62 |
| Novembre | 75 | 424 = 60 + 40 + 38 + 30 + 25 + 26 + 20 + 18 + 30 + 62 + 75 |
| Décembre | 90 | 514 = 60 + 40 + 38 + 30 + 25 + 26 + 20 + 18 + 30 + 62 + 75 + 90 |
La première colonne nous indique le nombre d'observations pour chaque mois, indépendamment des autres mois. La deuxième colonne nous donne le nombre d'observations à ce jour en additionnant les nombres ligne après ligne. Par exemple, pour janvier il y avait 60 observations de super-héros, de sorte que le total est 60. En février, il y avait 40 observations, ce qui signifie que le total est jusqu'à présent de 100 parce que les 40 observations de février se sont ajoutés aux 60 de janvier. Et ainsi de suite pour chaque mois qui suit.
Pourquoi faisons-nous tous ces calculs? Afin de les utiliser dans un graphe cumulatif.
Si vous créez un graphique cumulatif, il est important que vous en informiez vos lecteurs.
Pourquoi? Regardons ce graphique indiquant des données non cumulatives sur une base mensuelle:
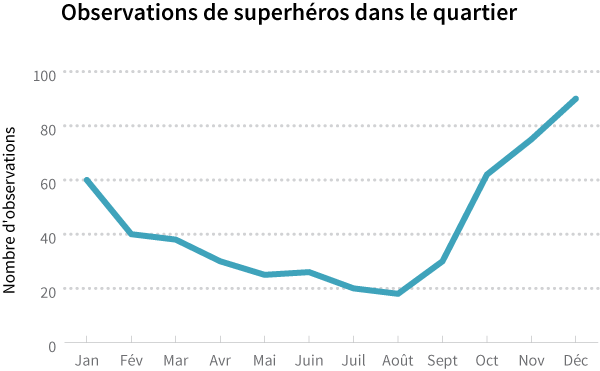
Notez le comportement de la ligne tracée: le nombre d'observations mensuelles diminue généralement au mois d’Août, puis augmente jusqu'à la fin de l'année. Les super héros sont apparemment plus occupés pendant les mois de vacances et viennent moins dans votre quartier.
Comparez maintenant le graphique ci-dessus de avec le graphique cumulatif ci-dessous:
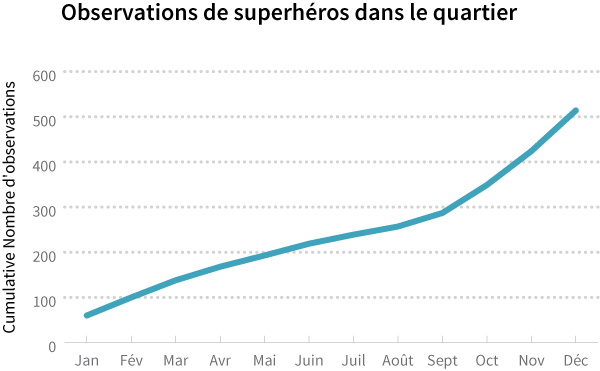
Vous remarquerez que la ligne tracée ne ressemble pas à la première. Celle du graphique cumulatif ne cesse d'augmenter parce que les chiffres ne cessent de s’ajouter les uns aux autres. Il est facile de regarder un graphique cumulatif et de penser à tort qu'il nous montre une tendance qui augmente systématiquement lorsque ce n’est pas vraiment le cas.
Il est ainsi important de prévenir votre public lorsque vous utilisez un graphe cumulatif afin d’éviter une mauvaise interprétation des données.
Contexte
Sans contexte, les histoires que nous essayons de raconter au travers de nos graphiques n’auront pas de point de référence sur lequel nous pourrons nous baser pour interpréter les différences. Par exemple, trouvez-vous que la tendance suivante est habituelle ou non?
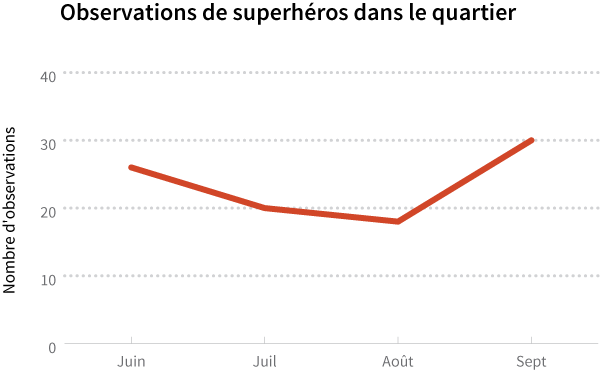
Alternativement, trop de données peuvent submerger une audience. Dans ce cas, le contexte est perdu parmi tous les renseignements et devient plutôt une vérité trop compliquée. Par exemple, n’est-il pas plus difficile de remarquer et d’analyser la ligne rouge dans le graphique ci-dessous?
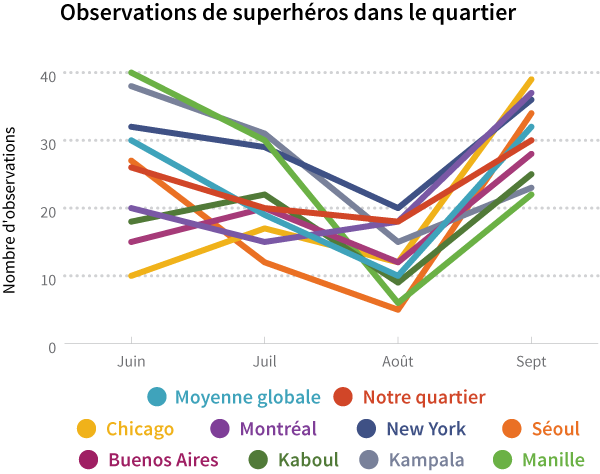
C’est pourquoi la visualisation des données est difficile! Vous devez comprendre comment présenter vos données d'une manière qui permette aux lecteurs de voir clairement les tendances et de comparer avec précision les différences. Par exemple, jetons un coup d'œil au graphique suivant:
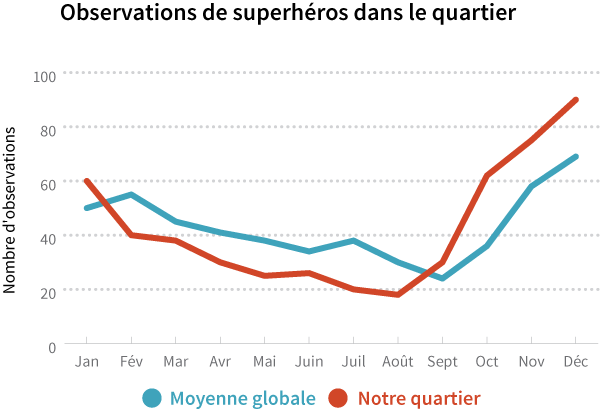
Si vous voulez montrer à votre audience à quel point le nombre d’apparitions de super-héros a changé au fil du temps, présenter les données sur un laps de temps annuel donne plus de contexte et est plus intéressant que sur un laps de temps mensuel. Et au lieu de montrer les courbes de tendance pour des dizaines de villes à travers le monde, votre graphique sera moins encombré et plus pertinent pour votre public si vous vous focalisez sur votre propre quartier par exemple. Une bonne pratique est aussi d’inclure un point de référence, par exemple une moyenne globale, afin que les voisins qui composent votre audience réalisent si leur quartier est typique ou non.
Le chapitre suivant et dernier de ce livre aura pour but de détailler d’une façon plus importante les règles liées au contexte et souligne d’autres façons graphiques pouvant induire en erreur un public. Rappelez-vous: être cohérent et transparent doit être la base de vos visualisations.