Chapitre 11
Transformations de données
Par Kiran PV
Adapté par Laurent Nepveu
Ce chapitre présente des concepts statistiques un peu plus avancés que ce qui a été proposé à travers les autres chapitres. Nous désirons tout de même inclure une brève introduction aux transformations de données, car il est possible que vous y aillez recours. Si vous devez appliquer des transformations à vos données, réferrez-vous à notre Appendix pour plus d'information.
Lorsqu'on prend une photo avec un appareil numérique, il arrive qu'il ne soit pas possible de bien distinguer chaque détails de la photo. Certaines couleurs peuvent être trop foncées ou trop pâles, la photo peut être floue, ou encore certains objets peuvent être tout simplement trop petits. Vous utiliserez alors un logiciel tel que Instagram ou Photoshop pour la modifier ou appliquer un filtre. Vous transformerez ainsi la photo pour rendre ces détails plus faciles à distinguer, pour la rendre plus claire et plus belle.
Fréquemment, les données que nous traitons doivent être ainsi transformées. Vous aurez peut-être un jeu de données qui, lorsque visualisé tel quel, ne revèle pas l'information qu'il contient véritablement ou ne permet pas de distinguer certaines caractéristiques clés des données. Il est aussi possible que vous désireriez effectuer des tests statistiques sur vos données, mais que celles-ci ne respectent pas les hypothèses quant aux distributions que plusieurs tests statistiques requièrent (par exemple, que la variable testée suive une loi normale). Appliquer des transformations à vos données est une façon de palier aux deux problèmes présentés. Nous présentons ici quelques transformations communes dont vous pourriez avoir besoin lorsque vous manipulerez et visualiserez vos données.
Les transformations de données consistent donc en des manipulations permettant de révéler certaines caractéristiques des données originales qui ne peuvent pas ou pas facilement être observées. On peut procéder à la transformation de la distribution d'une variable de nos données pour la rendre plus facilement observable ou encore pour qu'elle corresponde aux hypothèses des tests statistiques que nous voulons appliquer. Une technique très fréquente consistera à appliquer une fonction mathématique sur notre variable. Par exemple, on pourra utiliser, plutôt qu'une variable originale X, son logarithme ou encore sa racine carrée.
Attention! Ne jamais appliquer les transformations directement sur les données originales. Les variables transformées doivent être conservées dans de nouvelles variables dans votre jeu de données ou encore peuvent être placées dans un tout nouveau jeu de données. Vous ne savez jamais quand vous aurez besoin des données originales non-transformées à nouveau dans vos analyses ou vos visualisations.
Distribution normale et asymétrie des données
L'hypothèse la plus fréquente parmi tous les tests statistiques est celle qui requiert que la ou les variables analysées soient normalement distribuées. La distribution normale est aussi connue sous le nom de "courbe en cloche" (ou "bell curve" en anglais); On l'appelle ainsi parce que lorsque visualisées, les données prennent la forme d'une cloche de part et d'autre d'une valeur centrale. Par exemple, certaines mesures chez l'humain telles que la taille, le poids, la durée de vie ou encore les résultats de tests de QI sont généralement normalement distribuées autour d'une valeur moyenne de la population.
Une distribution normale est répartie également de part et d'autre d'une valeur moyenne centrale. La courbe est symétrique par rapport à la moyenne. Lorsque la distribution des données est déséquilibrée soit à gauche ou soit à droite, on dira qu'elle est biaisée. Dans ces cas, il y a plus de données d’un côté du sommet de la courbe que de l’autre. Des données biaisées à droite ont une longue queue qui s'étend à droite de la moyenne de la distribution tandis que des données biaisées à gauche ont une longue queue à gauche. Lorsque des données sont très biaisées, il peut être difficile de visualiser les extrêmes. Dans ce cas, une transformation vous permettra soit de procéder à des tests statistiques ou encore à mieux visualiser la distribution en entier.
Distribution normale
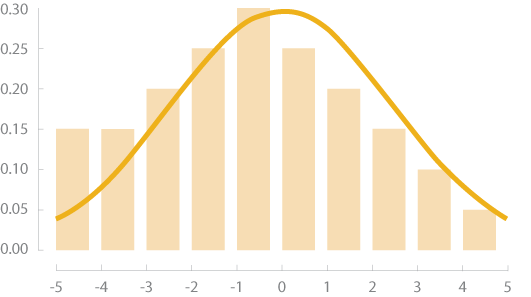
Désaxée vers la gauche
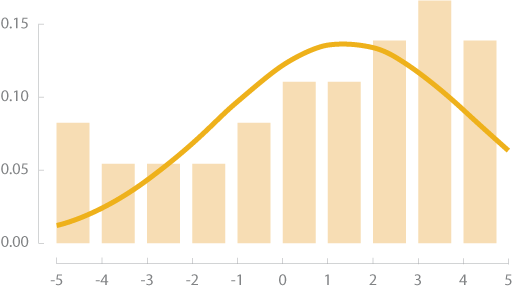
Désaxée vers la droite
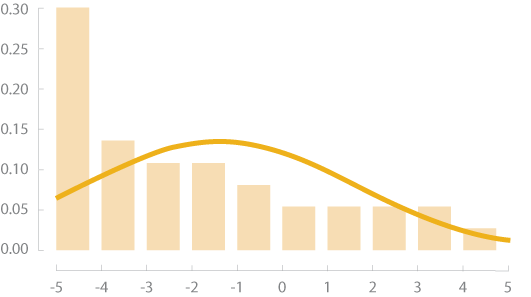
Un exemple de transformations avec un échantillon de données réelles
Considérons des données de population et de superficie des 50 états américains en 2012 pour comprendre comment les transformations de données peuvent vous aider à analyser et visualiser vos données. La première étape consiste à évaluer la distribution des variables analysées. C'est en évaluant la distribution de vos données brutes que vous déciderez si des transformations sont nécessaires. Pour se faire une idée de la distribution de nos données, débutons avec un histogramme de la variable de population et un nuage de points des variables de superficie et de population.
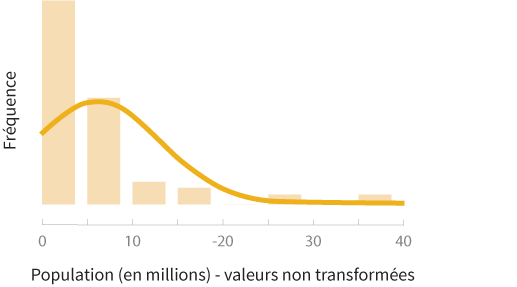
L'histogramme ci-dessus montre que la distribution de la variable de population est biaisée à droite. Ceci est attendu puisque la plupart des états américains ont une population de moins de 10 millions d'habitants. Il est donc clair que si nous voulons effectuer des tests statistiques qui requièrent une distribution normale, ces données devront être transformées.
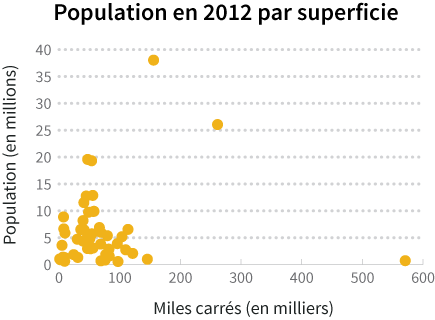
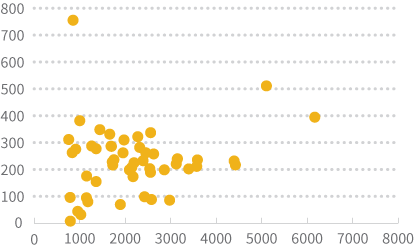
Le nuage de points ci-dessus présente la population sur l'axe des Y et la superficie sur l'axe des X. On y voit que la plupart des points sont concentrés entre 0 et 10 millions de population et sous les 400 000 kilomètres carrés. En utilisant les échelles non transformées, il est difficile de bien voir la relation entre la population et la superficie. Les valeurs hors normes (ou valeurs abérrantes) de l'Alaska et de la Californie font en sorte qu'on ne peut pas simplement agrandir les axes. Il faudra procéder à une transformation.
Plusieurs transformations peuvent être appliquées dans les deux cas précédents. Nous nous attarderons ici à quelques transformations les plus couramment utilisées pour vous aider à comprendre comment elles vous permettront de mieux visualiser vos données et d'approfondir votre analyse.
Transformation logarithmique
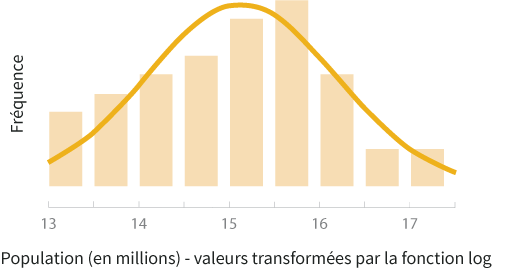
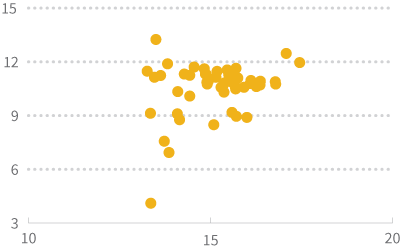
La transformation logarithmique consiste tout simplement à appliquer la fonction log à chacune des valeurs de la variable à transformer. Vous utilisez ensuite dans votre analyse la nouvelle variable constituée des résultats de la fonction log au lieu des données originales. Cette transformation a un impact marqué sur la distribution d'une variable. Elle permet en général de rapprocher des valeurs extrêmes pour obtenir des graphes de distribution moins étendus. Les deux graphes ci-dessous montrent d'une part la variable population à laquelle on a appliqué la fonction logarithme naturel et, d'autre part, le même nuage de points que précédemment, mais auquel on a appliqué la fonction logarithme naturel sur les deux variables de population et superficie.
Transformation racine carrée
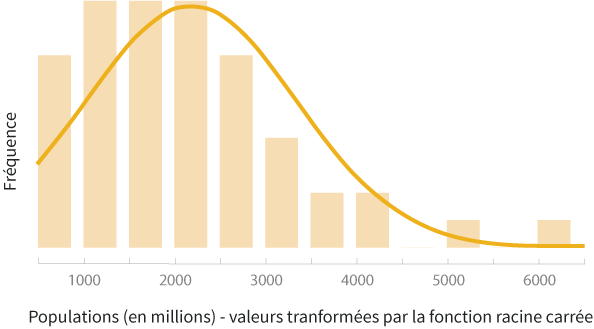
La transformation racine carrée consiste à calculer la racine carrée de chacune des valeurs d'une variable d'un jeu de données et d'utiliser cette résultante dans notre analyse. Cette transformation a un impact plus modéré sur la distribution. Les deux graphes ci-dessous montrent la distribution de la population à laquelle on a appliqué une racine carrée, ainsi que le nuage de points, toujours de la population par rapport à la superficie, auquel on a appliqué la racine carrée aux deux variables.
Choisir la bonne transformation
Une fois qu'on a acquis une bonne connaissance des différentes transformations que l'on peut appliquer, il faut développer une intuition pour choisir les transformations à utiliser dans différents contextes. Bien qu'il existe parfois des techniques formelles pour choisir une transformation, il est plus souvent nécessaire de procéder par essai et erreur pour choisir. Une stratégie simple consiste à essayer plusieurs transformations et de valider ensuite les résultats.
Considérez les histogrammes des données transformées ci-dessus. On peut facilement voir que la transformation logarithmique semble préférable à la racine carrée qui elle contient toujours un léger biais. Si vous effectuez un test statistique requérant une distribution normale, la transformation logarithmique est le meilleur choix.
Par contre, si votre but est plutôt de mieux visualiser la relation entre la population et la superficie des états, alors la racine carrée est une meilleure transformation car les données sont mieux dispersées sur le graphe.
Transformations communes
| Méthode | Fonction mathématique | À utiliser pour: | À éviter pour: |
|---|---|---|---|
| Log | ln(x) log10(x) |
Données biaisées à droite log10(x) est efficace lorsque les données sont distribuées sur des valeurs de plusieurs puissances de 10 (100, 1000, 10 000, etc.) | Valeurs de zéro Valeurs négatives |
| Carré root | √x | Données biaisées à droite | Valeurs négatives |
| Carré | x2 | Données biaisées à gauche | Valeurs négatives |
| Racine cubique | x1/3 | Données biaisées à droite Valeurs négatives |
Pas aussi efficace pour normaliser que la fonction log |
| Inverse | 1/x | Rapprocher les valeurs extrêmes des valeurs moyennes | Valeurs de zéro Valeurs négatives |
Avertissements quant à l'utilisation de transformations
Étant donné que les transformations de données nécessitent d'appliquer une fonction mathématique à vos variables, il faut être prudent lors de l'interprétation des résultats puisque ceux-ci auront changé d'échelle. Par exemple, en appliquant une transformation logarithmique à une variable de population, l'unité de la variable devient le log de la population. Lorsque vous présentez des résultats sur cette variable, il faut clairement communiquer que celle-ci a été transformée et quelle est la nouvelle échelle. Autrement, vos lecteurs considéreront que vous travaillez avec une donnée non transformée. Leur interprétation sera potentiellement erronée.
Si vous utilisez des données transformées pour calculer des paramètres statistiques comme la moyenne, il faut s'assurer de ramener le paramètre dans l'unité originale avant de présenter les résultats. Pour ramener cette moyenne dans l'unité originale, il suffit d'appliquer la fonction inverse de la transformation. Par exemple, si vous avez appliqué une racine carrée à vos données, il faut alors mettre au carrée le résultat pour le ramener dans l'unité d'origine.
Il est possible que vous n'utilisiez pas très souvent des transformations dans vos analyses. Par contre, lorsque vous le faites, il est important de bien connaître comment utiliser ces transformations et quels impacts elles sont sur vos données et votre analyse. La transformation des données n'est qu'un autre outil pour vous permettre de mieux exploiter vos données.